Les équations

L'écriture A=B s'appelle une égalité.
A s'appelle le premier membre de cette égalité et B son deuxième membre.
Par exemple: dans l'égalité: 5.x-8=3x+7; le premier membre est: 5.x-8 et le deuxième est 3.x+7.

Une équation est dite du premier degré à une seule inconnue si elle est de la forme: a.x=b telle que a et b sont deux nombres réels déterminés (connus) et que x est un nombre inconnue à quoi on doit chercher la valeur qui respecte l'égalité et si elle existe on l'appelera solution de cette equation. Comme par exemple considèrons l'équation: 3.x=12 la valeur de x qui respecte l'égalité n'est autre que: 4. On dit alors que 4 est la solution de l'équation: 3.x=12.

Il se peut qu'on aurait affaire à une équation qui n'est pas apparement de la forme a.x=b.
Si on peut la ramener (la transformer) sous la forme simlifiée a.x=b en appliquant les règles qui vont suivre alors elle est du premier degré à une seule inconnue

• 1) Dans une égalité on peut déplacer un terme d'un membre à l'autre à condition de lui changer son signe.
• 2) Dans une égalité on peut diviser ses membres par un même nombre non nul.

Appliquons ces deux règles dans l'équation (E): 7x-6=3x+9 .
7x-6=3x+9 est équivalente à 7x=3x+9+6 (on a déplacé -6 au deuxième membre en changeant son signe).
ce qui est équivalent aussi à 7x-3x=9+6 (cette fois ci on a déplacé 3x au premier membre en changeant son signe).
en simplifiant chaque membre de l'égalité obtenue on obtient alors: 4x=12 .
en multipliant maintenant chacun des membres par on obtient: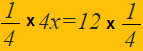
ce qui donne finalement par un simple calcul: .
La solution de l'équation (E) est alors: 3.